watonomous.github.io

[ Software Division : Object Tracking WIP ]

Created by [ Ankil Patel], last modified on May 09, 2020

The object tracking project is being rewritten (Object Tracking). The link posted has the preliminary strategy along with the pertinent information including why we need object tracking and some common pitfalls. I won't repeat it here to keep this doc concise.

A review of the existing literature points to several problems in this space to create robust trackers - we show the ones that are relevant to us:

associating new measurements to old tracked objects
conditioning object behavior to object properties (we're seeing the use of deep learning here)

While we don't see the need to incorporate deep learning techniques just yet, it should be said that feature vectors created using deep learning techniques have led to better performance in tracking.

Inputs

We assume that we have accurate bounding box points.

Unlike the previous iteration, we do not assume that the high level data fusion gives us input.

Outputs

We will output predicted bounding boxes for each frame that represents a better estimate of where objects are in the frame.

Objective

The goal of this project is to create an object tracking pipeline that can robustly track objects in, at-worst, constant acceleration and constant turn-rate scenarios.

High-level Overview

It's still undecided of whether we want to make this a separate process or a library. As a result, we'll make the project flexible enough to adapt to either or both situations. The high level diagram describing our general workflow is given below:

[

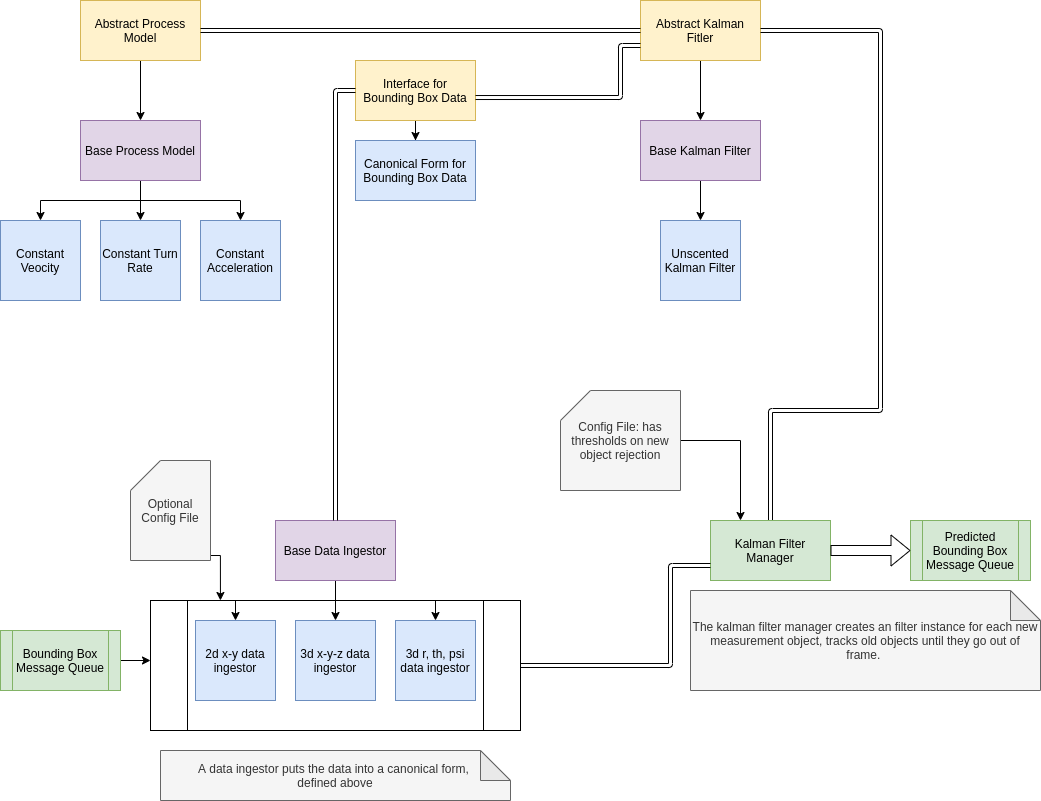
The arrows represent dependencies and the double lines represent codependency. (I'll fix it to uml later)

We pull bounding boxes from the Bounding Box Message Queue into our data ingestor which, using the canonical form of the bounding box, translates the incoming data to a format that is easier to work with and allows us to make certain assumptions about the image frame. The measurements go to a kalman filter manager which will create a new kalman filter instance if the measurement can't be assigned to a currently tracked object or will assign the new measurement to an existing tracked object. Each tracked object is packaged as a ros message and sent to the predicted bounding box message queue.

The kalman filter depends on a process model which describes the object behavior, or at least our perception of the object behavior.

Kalman Filter

The kalman filter library is modified from https://github.com/mherb/kalman. The modifications are as follows:

removed extended kalman filter implementation - we use the ukf implementation
removed unsafe filters - we use square root decomposition

There is a preference for unscented kalman filters instead of extended kalman filters since the sensor data might be warped and thus has high non-linearity or the object behavior is highly nonlinear and the EKF is unable to correctly track the object. We don't need to pay a computation cost like with particle swarm and we can reasonably assume gaussian noise. The computation cost for ukf is more than the cost for ekf, however, the benefits seem to be worth it (benchmark needed). It's also important to define what we mean by unsafe. We want our kalman filter to be numerically stable and ideally, we want to avoid or at least handle situations that lead to incorrect results. This idea is explained in the below section excerpt from Wikipedia:

[]{.aui-icon .aui-icon-small .aui-iconfont-info .confluence-information-macro-icon}

One problem with the Kalman filter is its numerical stability. If the process noise covariance Q~k~ is small, round-off error often causes a small positive eigenvalue to be computed as a negative number. This renders the numerical representation of the state covariance matrix P indefinite, while its true form is positive-definite.

Positive definite matrices have the property that they have a triangular matrix square root P = S·S^T^. This can be computed efficiently using the Cholesky factorization algorithm, but more importantly, if the covariance is kept in this form, it can never have a negative diagonal or become asymmetric. An equivalent form, which avoids many of the square root operations required by the matrix square root yet preserves the desirable numerical properties, is the U-D decomposition form, P = U·D·U^T^, where U is a unit triangular matrix (with unit diagonal), and D is a diagonal matrix.

Between the two, the U-D factorization uses the same amount of storage, and somewhat less computation, and is the most commonly used square root form. (Early literature on the relative efficiency is somewhat misleading, as it assumed that square roots were much more time-consuming than divisions,^[32]:69^ while on 21-st century computers they are only slightly more expensive.)

Efficient algorithms for the Kalman prediction and update steps in the square root form were developed by G. J. Bierman and C. L. Thornton.^[32]^

The L·D·L^T^ decomposition of the innovation covariance matrix S~k~ is the basis for another type of numerically efficient and robust square root filter.^[34]^ The algorithm starts with the LU decomposition as implemented in the Linear Algebra PACKage (LAPACK). These results are further factored into the L·D·L^T^ structure with methods given by Golub and Van Loan (algorithm 4.1.2) for a symmetric nonsingular matrix.^[35]^ Any singular covariance matrix is pivoted so that the first diagonal partition is nonsingular. The pivoting algorithm must retain any portion of the innovation covariance matrix directly corresponding to observed state-variables H~k~·x~k|k-1~ that are associated with auxiliary observations in y~k~. The l·d·l^t^ square-root filter requires orthogonalization of the observation vector.^[33]^ This may be done with the inverse square-root of the covariance matrix for the auxiliary variables using Method 2 in Higham (2002, p. 263).

The forked repo is kept on my personal github account and we will copy the repo's contents to gitlab once we feel we're confident with the approach: https://github.com/AnkilP/kalman
To access the doxygen documentation, run the following in terminal:
\

sudo apt install doxygen -y
sudo apt install graphviz -y

cd prediction/tracker/kalman_filter

doxygen -u Doxyfile 
doxygen Doxyfile

cd documentation/html
firefox index.html

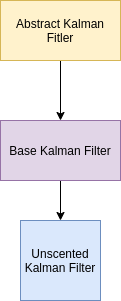
While the doxygen doc will have a more detailed description of the kalman filter, we show the following so that you can get a sense of what we can change - we can add normal extended kalman filters (normal means we don't do square root decomposition) and square root EKF as well as normal UKF. If we do benchmarking, we'll be able to determine what the bottlenecks are and then make a decision on what kind of kalman filter we want. For now, we're making a decision to use a square-root UKF.

[

Bounding Box

We need a canonical form for the bounding box that is consistent for the kalman filter so it is easier to work with and allows us to make certain assumptions about the image frame.

[

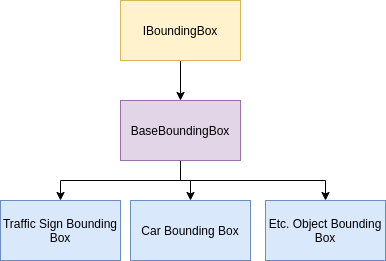
Each bounding box instance is applied to each bounding box to convert it to canonical form - you might recognize this as the visitor pattern (each bounding box data from the queue is visited by the corresponding bounding box instance to convert it to canonical form).

The canonical form itself is still up for consideration - for now, it will have to conform to Eigen (the linalg library) vectors that represent a state vector that the kalman filter class will use organically.

Data Ingestor

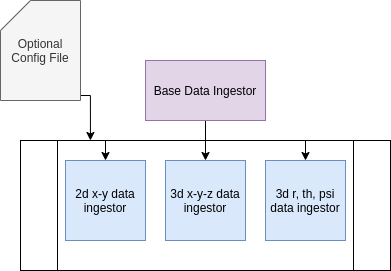
Depending on what type of data is in the bounding box queue, the data ingestor will need to apply the correct transformation to the bounding box data before it sends it to the kalman filter manager. We have three different types of ingestors for each type of data: 2d x-y, 3d x-y-z, 3d r-th-psi. For warped sensor data, we might be using 3d r-th-psi instead of the 3d x-y-z since it will be easier to track the objects (ref needed

this is mostly based on intuition). We specify the option to get input from a configuration file to specify rules on how bounding boxes are processed.

[

Process Model

The process model specifies the object behavior, of which we expect the following cases:

Case Model Used ——————————————- ——————————————- Object Stationary, Ego Vehicle Stationary Constant Velocity Object Stationary, Ego Vehicle Moving Constant Acceleration/ Constant Turn rate Object Moving, Ego Vehicle Stationary Constant Acceleration/ Constant Turn Rate Object Moving, Ego Vehicle Moving Constant Acceleration/ Constant Turn Rate

We propose the following design:

[

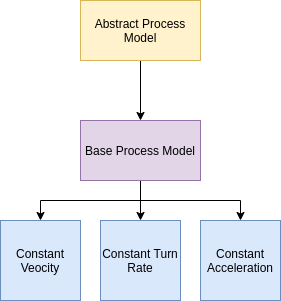
Ideally, kalman filters with different process models are used to track the movement of different objects and we can determine which process model to use based on the error.

Kalman Filter Manager

The manager tracks multiple objects and sends the location of the objects to a downstream application.

[

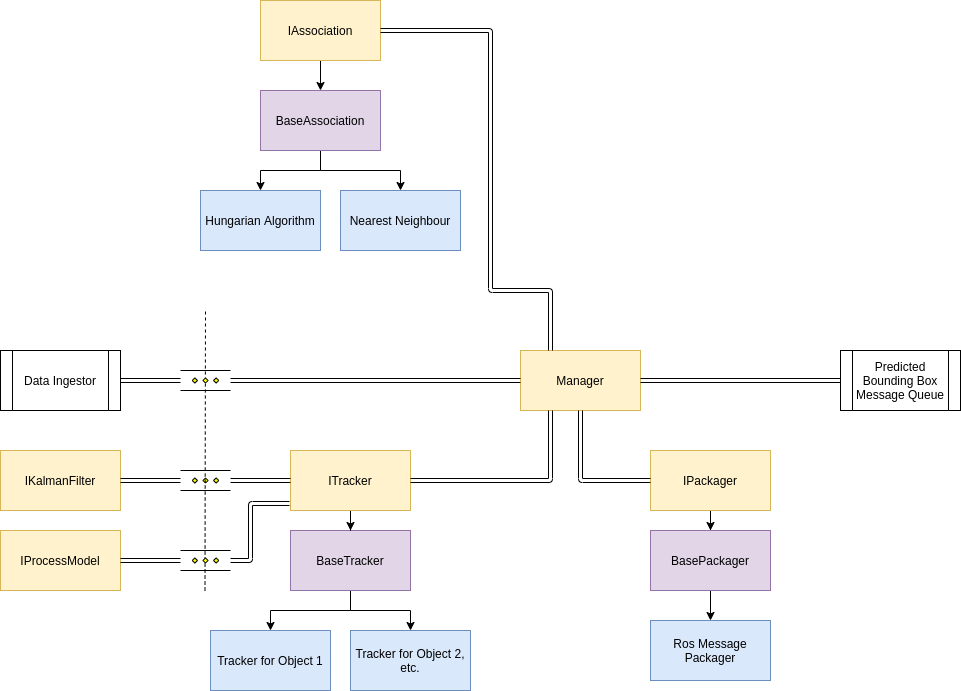
The manager has several responsibilities:

Track existing objects until they leave the image frame
Match new measurements to new trackers or existing objects
Package the results for each tracked object and push it to a queue
Maintain a consistent view of the world (same time)

The association of new measurements to existing tracked objects is handled by an association class which produces some matching (e.g. via the Hungarian algorithm or nearest neighbor). The tracker creates an ensemble of kalman filters using different process models ( we can have soft and hard thresholds for the prediction error to determine when we run the incorrect process model) and runs the update function with a new measurement from the manager. The manager also decides when the tracker instance needs to be unregistered. It would probably be a good idea if we created a pool of trackers instead of creating and deleting objects during run time. The manager could also synchronize the trackers so we have a consistent view of the object locations. After each time step, the ros message packager or some other packager will transform the state vectors into an appropriate ros message and publish them.

Notes

We could split the manager so that we can specify the sync logic.

Should we track centroids of the bounding boxes or the points of the bounding boxes? One of the benefits of tracking each individual point is that we could see how the bounding box deforms to measure the efficacy of the process model.

Attachments:

Object_Tracking (1).png (image/png)
Object_Tracking.png (image/png)
BoundingBox.png (image/png)
data_ingestor.png (image/png)
process.png (image/png)
manager.png (image/png)
manager (1).png (image/png)
manager (2).png (image/png)
kalma.png (image/png)
kalma.png (image/png)\

Document generated by Confluence on Dec 10, 2021 04:02

Atlassian